ポリゴンを回転させるには、ポリゴンの頂点座標を修正すればよい。しかし、90度、180度、270度の回転なら、4つの頂点座標を入れ替えるだけなのでプログラミングも楽だが、それ以外の角度で回転させようとすると、回転させる角度によって頂点座標を計算しなければならず、面倒である。
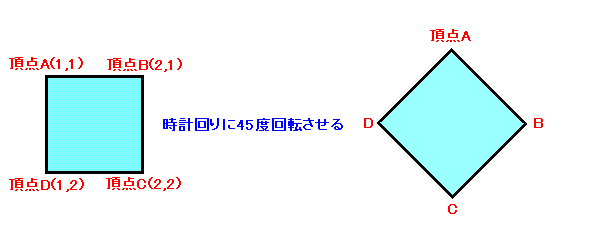
三角関数を使って求めることは可能だが・・・
ポリゴンを回転させるには、ポリゴンの頂点座標を修正すればよい。しかし、90度、180度、270度の回転なら、4つの頂点座標を入れ替えるだけなのでプログラミングも楽だが、それ以外の角度で回転させようとすると、回転させる角度によって頂点座標を計算しなければならず、面倒である。

三角関数を使って求めることは可能だが・・・
ポリゴンを回転するには個々の頂点を演算するより、行列を用いるのが簡単である。
行列にはX軸回転行列、Y軸回転行列、Z軸回転行列があるが、2DゲームではZ軸回転行列を使用する。
これをプログラムで表すと、次のようになる。
// ラジアンの初期化 float PAD = 3.141592f / 180.0f; // 行列の定義 D3DXMATRIX PosMatrix; // 頂点行列 D3DXMATRIX RotateMatrix; // 回転行列 // 行列の初期化(単位行列生成) D3DXMatrixIdentity(&PosMatrix); D3DXMatrixIdentity(&RotateMatrix);
※ラジアンとは角度の単位で、180度をπとして表す。つまり、180度=πであり、1度=π/180となる。sinやcosなど三角関数を使用する際に用いる角度はラジアン値であるため、1度は1*π/180となり、45度なら45*π/180というように計算し、ラジアン値を求める。
// 回転行列に角度を設定 D3DXMatrixRotationZ(&RotateMatrix, 角度(0〜360)* PAD);
// 拡大/縮小処理
int i;
for ( i=0 ; i < 4 ; i++ ) {
// 現在の頂点座標を格納
D3DXMatrixTranslation(&PosMatrix, MyChara.v[i].x, MyChara.v[i].y, MyChara.v[i].z);
// 演算
PosMatrix *= RotateMatrix;
// 演算結果を戻す
MyChara.v[i].x = PosMatrix._41; // 演算結果をポリゴンのX座標に格納
MyChara.v[i].y = PosMatrix._42; // 演算結果をポリゴンのY座標に格納
MyChara.v[i].z = PosMatrix._43; // 演算結果をポリゴンのZ座標に格納
}
移動処理、拡大/縮小処理と同様に、回転処理も関数化したほうが使いやすい。回転を行う関数を次のように作成する。NKC_Public.cppに作成するのがよいだろう。
//----------------------------------------------------------------------------------------
// 関数名 : RotateMatrix()
// 機能概要: 各頂点に対し、行列を使用して回転を行う
//----------------------------------------------------------------------------------------
void RotateMatrix(LPTLVERTEX v, int Rotate)
{
float PAD = 3.141592f / 180.0f; // ラジアンの初期化
D3DXMATRIX PosMatrix, RotateMatrix;
int i;
// 行列の初期化(単位行列生成)
D3DXMatrixIdentity(&PosMatrix);
D3DXMatrixIdentity(&RotateMatrix);
// 回転行列に角度を設定
D3DXMatrixRotationZ(&RotateMatrix, (float)Rotate * PAD);
// 回転処理
for ( i=0 ; i<4 ; i++ ) {
// 現在の頂点座標を格納
D3DXMatrixTranslation(&PosMatrix, v[i].x, v[i].y, v[i].z);
// 演算
PosMatrix *= RotateMatrix;
// 結果を戻す
v[i].x = PosMatrix._41;
v[i].y = PosMatrix._42;
v[i].z = PosMatrix._43;
}
}
MoveMatrix()関数を作成したら、この関数を使用してポリゴンの拡大/縮小が行われるかを確認する。例えば'A'キーを押すと角度を1度増やし、'S'キーを押すと角度を1度減らすようにプログラムすると、次のようになる。
//--------------------------------------------------- 回転テスト if ( gl_KeyTbl['S'] & 0x80 ) RotateMatrix(MyChara.Vertex, 1); if ( gl_KeyTbl['A'] & 0x80 ) RotateMatrix(MyChara.Vertex, -1);
※任意のプログラムに上記修正を行い、'A'キーを押すと拡大、'S'キーを押すと縮小されることを確認すること。
拡大/縮小と同様、回転は原点(0, 0)を中心に行われる。よって、ポリゴンの中心を原点として回転が行われるよう、回転処理関数を次のように修正する。
//----------------------------------------------------------------------------------------
// 関数名 : RotateMatrix()
// 機能概要: 各頂点に対し、行列を使用して回転を行う
//----------------------------------------------------------------------------------------
void RotateMatrix(LPTLVERTEX v, int Rotate)
{
float PAD = 3.141592f / 180.0f; // ラジアンの初期化
D3DXMATRIX PosMatrix, RotateMatrix;
float x1, y1;
int i;
// ポリゴンの中心を求め、原点へ移動させる
x1 = (v[2].x - v[0].x) / 2.0f + v[0].x;
y1 = (v[3].y - v[1].y) / 2.0f + v[1].y;
MoveMatrix(v, -x1, -y1, 0.0f);
// 行列の初期化(単位行列生成)
D3DXMatrixIdentity(&PosMatrix);
D3DXMatrixIdentity(&RotateMatrix);
// 回転行列に角度を設定
D3DXMatrixRotationZ(&RotateMatrix, (float)Rotate * PAD);
// 回転処理
for ( i=0 ; i<4 ; i++ ) {
// 現在の頂点座標を格納
D3DXMatrixTranslation(&PosMatrix, v[i].x, v[i].y, v[i].z);
// 演算
PosMatrix *= RotateMatrix;
// 結果を戻す
v[i].x = PosMatrix._41;
v[i].y = PosMatrix._42;
v[i].z = PosMatrix._43;
}
// ポリゴンを元の位置へ戻す
MoveMatrix(v, x1, y1, 0.0f);
}
※回転処理関数(RotateMatrix関数)を修正し、ポリゴンの中心座標が変わることなく回転が行われることを確認する。
| BACK(拡大・縮小) |