行列を用いた移動

ポリゴンを上下左右に移動させるには、ポリゴンの各頂点座標にそれぞれ移動させたい値を加えればよい。
例えば、頂点Ａ、Ｂ、Ｃ、Ｄで構成されるポリゴンを右方向に１０ピクセル移動させたいなら、ポリゴンの各頂点のｘ座標に対して次の演算を行えばよい。

頂点ＡのＸ座標　＝　頂点ＡのＸ座標　＋　１０．０ｆ
頂点ＢのＸ座標　＝　頂点ＢのＸ座標　＋　１０．０ｆ
頂点ＣのＸ座標　＝　頂点ＣのＸ座標　＋　１０．０ｆ
頂点ＤのＸ座標　＝　頂点ＤのＸ座標　＋　１０．０ｆ

各頂点のＸ，Ｙ座標にそれぞれ移動量を加えるのは面倒なので、移動処理を行う関数（Move関数）を用意し、その関数を使って簡単に移動処理が行えるようにした（６章１を参照）。
先の例の場合、Move()関数を使って次のようにプログラムできる。

Move(VertexDataTbl1, 10.0f, 0.0f);

上記で行ったように、各頂点ごとに演算をして移動先の座標を求める方法以外に、行列（マトリックス）を用いて頂点座標を求める方法がある。
ポリゴンを移動させるだけなら演算で移動先の座標を簡単に求めることができるが、行列を使えば移動、拡大／縮小、回転が１回の乗算だけで行うことができる。
この授業では２Ｄゲームの製作を目標にしているため、行列を使わなくても特に支障はない。しかし、３Ｄゲームの製作には欠かすことのできない技術であるため、ここでは行列を使ってポリゴンを移動させる方法を紹介する。２Ｄで行列の移動が使えれば、３Ｄゲームの授業についていくことができるだろう。

行列については数学の授業で詳しく行うので、ここでは簡単な紹介だけにしておく。
頂点Ａ（０，０，０）をＸ方向に１０移動させると、頂点Ａ’は（１０，０，０）になる。この演算を行列で行うには、頂点行列に移動量行列を乗算すればよい。
それぞれの行列は４行４列で表すと決まっており、次のように表現される。

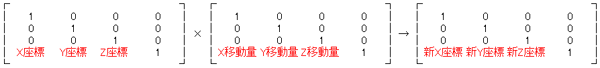
これをプログラムで表すと、次のようになる。

1.変数の宣言

// 行列の定義
D3DXMATRIX PosMatrix;  // 頂点行列
D3DXMATRIX MoveMatrix; // 移動量行列

《POINT》

• D3DXMATRIX型は３Ｄ用の行列型で、４行４列の行列が用意される。
• 頂点座標を格納する「PosMatrix」と、移動量を格納する「MoveMatrix」変数をそれぞれ宣言する。

2.行列に値を設定

// 行列の初期化
D3DXMatrixIdentity(&PosMatrix);  // 単位行列生成
D3DXMatrixIdentity(&MoveMatrix); // 単位行列生成
// 移動量行列に移動量を設定
MoveMatrix._41 = 10.0f; // Ｘ移動量
MoveMatrix._42 = 0.0f; // Ｙ移動量
MoveMatrix._43 = 0.0f; // Ｚ移動量

《POINT》

• 宣言した行列を、単位行列（行列において数字の１と同じ意味。他の行列と乗算を行っても結果は変わらないいう性質を持つ）という形で初期化する。
• Ｘ移動量は４行１列に、Ｙ移動量は４行２列に、Ｚ移動量は４行３列にそれぞれ格納する。この場合、Ｘ座標に10.0fの移動量をセットし、Ｙ，Ｚ座標は変化させない。

3.移動処理（MyChara.v[0〜3]に、現在のポリゴンの座標がセットされているものとする）

// 移動処理
int i;
for ( i=0 ; i < 4 ; i++ ) {
    PosMatrix._41 = MyChara.v[i].x; // 頂点行列に現在のポリゴンのＸ座標をセット
    PosMatrix *= MoveMatrix;        // 頂点行列に移動量を加算
    MyChara.v[i].x = PosMatrix._41; // 演算結果をポリゴンのＸ座標に格納
}

《POINT》

• 四角形ポリゴンは４つの頂点を持つため、０から３までループさせる。
• 今回はＸ座標のみを移動させるため、各頂点のＸ座標を頂点行列（PosMatrix）にセットしてから、移動量行列を乗算し、結果を頂点情報に戻している。

上記のやり方では、行列への座標／移動量のセットは、行列に値を直接代入している。例えば四角形ポリゴンのＸ，Ｙ座標を同時に移動させる場合、次のようなプログラムになる。

// 移動量のセット
MoveMatrix._41 = Ｘ方向の移動量;
MoveMatrix._42 = Ｙ方向の移動量;

// 移動処理
int i;
for ( i=0 ; i < 4 ; i++ ) {
    // 頂点情報のセット
    PosMatrix._41 = MyChara.v[i].x;
    PosMatrix._42 = MyChara.v[i].y;
    // 演算
    PosMatrix *= MoveMatrix;
    // 結果を戻す
    MyChara.v[i].x = PosMatrix._41;
    MyChara.v[i].y = PosMatrix._42;
}

これは、D3DXMatrixTranslation関数を使って次のように簡略化できる。

// 移動量のセット
D3DXMatrixTranslation(&MoveMatrix, Ｘ方向の移動量, Ｙ方向の移動量, Ｚ方向の移動量);

// 移動処理
int i;
for ( i=0 ; i < 4 ; i++ ) {
    // 頂点情報のセット
    D3DXMatrixTranslation(&PosMatrix, MyChara.v[i].x, MyChara.v[i].y, MyChara.v[i].z);
    // 演算
    PosMatrix *= MoveMatrix;
    // 結果を戻す
    MyChara.v[i].x = PosMatrix._41;
    MyChara.v[i].y = PosMatrix._42;
}

//----------------------------------------------------------------------------------------
// 関数名　：　MoveMatrix()
// 機能概要：　各頂点に対し、行列を使用して与えられた移動量を加算する
//----------------------------------------------------------------------------------------
void MoveMatrix(LPTLVERTEX v, float x, float y, float z)
{
    D3DXMATRIX PosMatrix, MoveMatrix;
    int i;

    // 行列の初期化（単位行列生成）
    D3DXMatrixIdentity(&PosMatrix);
    D3DXMatrixIdentity(&MoveMatrix);

    // 移動量設定
    D3DXMatrixTranslation(&MoveMatrix, x, y, z);

    // 移動処理
    for ( i=0 ; i<4 ; i++ ) {
        // 現在の頂点座標を格納
        D3DXMatrixTranslation(&PosMatrix, v[i].x, v[i].y, v[i].z);
        // 演算
        PosMatrix *= MoveMatrix;
        // 結果を戻す
        v[i].x = PosMatrix._41;
        v[i].y = PosMatrix._42;
        v[i].z = PosMatrix._43;
    }

}

Move(MyChara.v, MyChara.MoveX, MyChara.MoveY);
↓
MoveMatrix(MyChara.v, MyChara.MoveX, MyChara.MoveY, 0.0f);